Author: Arnel C. Reyes
Published: 06 September 2024
Last Updated: 07 September 2024
Cryptographic approaches are essential techniques used to protect data, ensure privacy, and establish secure communication in digital systems. These techniques can be broadly categorized into symmetric encryption, asymmetric encryption, hybrid methods combining both, and enhanced methods with digital signatures and hashing algorithms for added security and authentication to achieve confidentiality, integrity, authentication, and non-repudiation in data transmission.
- Symmetric Cryptography involves using a single secret key for both encryption and decryption of data. It is efficient for processing large amounts of data.
- Asymmetric Cryptography uses a pair of keys—a public key for encryption and a private key for decryption—allowing secure communication without the need to share secret keys beforehand.
- Hybrid Approaches combine symmetric and asymmetric methods, where symmetric encryption secures the data, and asymmetric encryption secures the symmetric key exchange.
- Digital Signatures utilize asymmetric cryptography and hash functions to authenticate the sender's identity and ensure the message's integrity.
By integrating these methods, cryptographic systems can provide secure, efficient, and authenticated communication over insecure networks.
Background
Cryptography has a long history, evolving from simple manual ciphers like Caesar’s cipher to complex algorithms designed for the digital age. Early cryptographic methods were primarily symmetric, requiring secure key exchanges, which posed challenges as networks expanded. The development of asymmetric cryptography in the 1970s, such as RSA, provided a revolutionary solution for secure key distribution in open networks like the internet. This led to the creation of hybrid cryptography, where symmetric encryption handles the data, and asymmetric cryptography secures key exchanges.
The growing need for data integrity and authentication gave rise to digital signatures, ensuring not only the privacy of information but also the authenticity of the sender and the integrity of the data. This combination of encryption and signature methods has become standard in securing web traffic (TLS/SSL), emails (PGP, S/MIME), financial transactions, and legal documentation
The evolution of cryptographic approaches has been driven by the need to secure information in increasingly complex and interconnected environments.
- Early Cryptography: Initially, cryptography was primarily symmetric, with examples like the Caesar cipher. The main challenge was securely sharing the secret key between parties.
- Asymmetric Cryptography Revolution: In the 1970s, the development of asymmetric cryptography, such as RSA, addressed the key distribution problem by introducing key pairs (public and private keys). This allowed secure exchanges without pre-shared secrets but at the cost of computational efficiency.
- Hybrid Systems: To leverage the efficiency of symmetric encryption and the secure key distribution of asymmetric encryption, hybrid systems were developed. Protocols like TLS/SSL use asymmetric encryption to securely exchange symmetric keys, which then encrypt the actual data transfer efficiently.
- Digital Signatures and Hash Functions: The addition of digital signatures and cryptographic hash functions enhanced security by providing mechanisms for authentication and integrity verification. Hash functions produce a unique digest of the data, and digital signatures created using a sender's private key allow recipients to verify the sender's identity and confirm that the message has not been altered.
- Modern Applications: These cryptographic approaches are foundational in contemporary security protocols and applications, including secure web browsing (HTTPS), email security (PGP, S/MIME), virtual private networks (VPNs), and secure financial transactions.
Symmetric cryptography uses the same secret key to encrypt and decrypt data. The key must be shared securely between the sender and receiver to enable secure communication.
Symmetric encryption is widely used due to its efficiency in encrypting large amounts of data. Historically, symmetric encryption methods, like the Caesar cipher, were used for secure communication. Modern symmetric algorithms, like AES (Advanced Encryption Standard), offer strong security and are implemented in various applications like VPNs, disk encryption, and secure communication protocols such as TLS.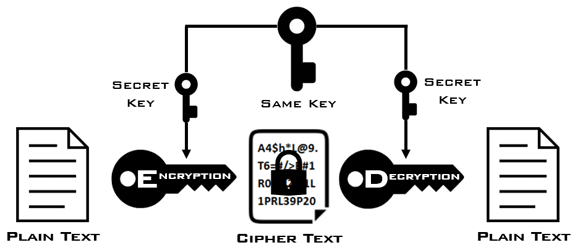
Example Application in Python
| # Filename: symmetric.py from cryptography.hazmat.primitives import hashes from cryptography.hazmat.primitives.kdf.pbkdf2 import PBKDF2HMAC from cryptography.fernet import Fernet import base64 # Shared key (convert 'secret' to a valid key for Fernet) password = b"secret" # Shared key salt = b"salt1234" # Salt (this can be shared, but should be consistent) # Derive a key using PBKDF2HMAC (key derivation function) kdf = PBKDF2HMAC( algorithm=hashes.SHA256(), length=32, salt=salt, iterations=100000, ) key = base64.urlsafe_b64encode(kdf.derive(password)) # Derive the key cipher = Fernet(key) # Encrypt a message message = b"Hello, World!" encrypted_message = cipher.encrypt(message) print(f"Encrypted: {encrypted_message}") # Decrypt the message decrypted_message = cipher.decrypt(encrypted_message) print(f"Decrypted: {decrypted_message.decode()}") |
Output:
| $ python symmetric.py Encrypted: b'gAAAAABm2-JQ4J1FcRoh15b6fPqcDMAnFYQxXHjQlu0ucNDrzYKqbx4QljvucSHvFHbtAIkmnijgRiasWvojanrwyPubRl3BkQ==' Decrypted: Hello, World! |
Examples of Symmetric Cryptography
- AES (Advanced Encryption Standard): A widely used encryption algorithm that is both fast and secure, AES is the standard for securing sensitive data. It is used in various protocols, including SSL/TLS for securing web traffic, and is trusted for both government and private sector encryption.
- DES (Data Encryption Standard): An older symmetric encryption algorithm developed in the 1970s, DES uses a 56-bit key, which has since been deemed insecure due to vulnerabilities to brute-force attacks. DES has largely been replaced by AES, but it paved the way for modern encryption standards.
- 3DES (Triple Data Encryption Standard): A more secure variant of DES, 3DES applies the DES algorithm three times to each data block with different keys, providing greater security. However, it is slower than modern encryption algorithms like AES and has also been deprecated for many uses due to performance limitations.
- Blowfish: A fast block cipher designed to replace DES, Blowfish uses variable key lengths (32 to 448 bits) and is known for its speed in software. It is used in applications like password management tools but has been succeeded by more secure algorithms.
- Twofish: The successor to Blowfish, Twofish is a symmetric encryption algorithm known for its flexibility and high speed. It uses a block size of 128 bits and key sizes up to 256 bits. Twofish was a finalist in the AES competition but was not chosen; however, it remains a strong and efficient alternative.
- RC4 (Rivest Cipher 4): A stream cipher that was widely used in protocols like WEP (for Wi-Fi security) and SSL. While RC4 was fast and simple, vulnerabilities were discovered, leading to its deprecation in favor of more secure algorithms like AES.
- ChaCha20: A modern stream cipher designed as a faster and more secure alternative to RC4. ChaCha20 is widely used in modern encryption systems like Google’s TLS implementation and is noted for its speed, even on low-power devices.
- IDEA (International Data Encryption Algorithm): A block cipher known for its strong encryption with a 128-bit key. IDEA was widely used in earlier versions of PGP (Pretty Good Privacy) for encrypting emails but has been largely replaced by more advanced algorithms like AES.
Symmetric cryptography is highly efficient and suitable for encrypting large data sets. Its main drawback is the need for secure key distribution, as both parties must have the same key in advance.
Asymmetric cryptography involves using a public key for encryption and a private key for decryption. The public key can be shared openly, while the private key must remain secret.
Asymmetric cryptography was developed in the 1970s to solve the problem of secure key exchange in symmetric encryption. It is slower than symmetric encryption but enables secure communication without needing a shared secret key. Asymmetric cryptography is primarily used for securing data exchanges, such as in HTTPS, where public keys encrypt session keys.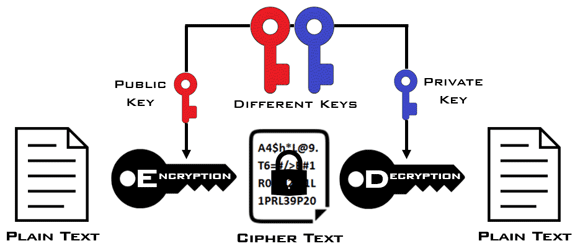
Example Application in Python
| # Filename: asymmetric.py from cryptography.hazmat.primitives.asymmetric import padding from cryptography.hazmat.primitives import hashes, serialization # Load the public key from file with open("public_key.pem", "rb") as f: public_key = serialization.load_pem_public_key(f.read()) # Load the private key from file with open("private_key.pem", "rb") as f: private_key = serialization.load_pem_private_key(f.read(), password=None) # Encrypt a message message = b"Simple secret message" encrypted = public_key.encrypt( message, padding.OAEP(mgf=padding.MGF1(algorithm=hashes.SHA256()), algorithm=hashes.SHA256(), label=None) ) # Decrypt the message decrypted = private_key.decrypt( encrypted, padding.OAEP(mgf=padding.MGF1(algorithm=hashes.SHA256()), algorithm=hashes.SHA256(), label=None) ) # Output print("Encrypted:", encrypted) print("Decrypted:", decrypted.decode()) |
Output:
| $ python asymmetric.py Encrypted: b'8t\x04\xfc\xd38\x8aF\xf5=\xf1\xb5\xbe\x0e\xf5\xe6M\x05H\x1d\x07\x93\xd9\xc9\x9bp=don\xc7\xd4\xf3\xe6\xccpX \xaf-\xc0KX\xd5!\xbb7}\xa0\xe2\xf4\x1bi6y!R@\x94D\xe7\xfc\x90A\xba,\xc0\x14\x80%P\x06c\x03\xa0OX\xab^\x8f\xfc\xcf\x18\x cf\x0b!7ld\x8d\xac}\xc5\xa4)\xa5\xb8\x0f3\xc6\xeb\x0b\x9e\x0bM\x0c\x80\xa8U\xe1\xad\xa4\xa9\n\xcf\xfb\xfbN\x85\x0e\xf2$ #$\x9dX\xb8\x02;\xc0\xc9,+\xe4\xa4U\xb6Rf\xa7\x03\x07\xa5\xc5~\xc9\x8c\x9e\xdc\xaf\xa67\xa9V\x7f\xd3\xb6A\xdcb)\xdf\x10 \x89i\xe3\x9eT\xf3Lv\x9e\xbb:?\xc7\xf8\x87k{\xc3\xd3\x85\x84@\xce\xd6\x08\xb5~U%\xec\xa9Z\x90\xbfY/[V\x9d9\xdd|\xe0\xeb \xecO\xf3%\xa482\xc0\xe6\xe5\xc1\x8d\xce^m>\x02\x12\xe0\x9b(\x87!^\\\xbf\x8b\xcd\xde/\xc1\xc6h\x87\xd4\x83\xfc%U\x02B|$ A\x8e\x8f\xddAv\x84' Decrypted: Simple secret message |
Examples of Asymmetric Cryptography
- RSA (Rivest-Shamir-Adleman): One of the most widely used public-key encryption systems, RSA is employed for secure data transmission, especially in digital signatures and key exchange protocols like TLS/SSL. It uses large integer factorization for security, with key sizes typically ranging from 2048 to 4096 bits.
- ECC (Elliptic Curve Cryptography): A modern asymmetric encryption algorithm based on elliptic curves, ECC provides similar security to RSA but with much smaller key sizes, making it faster and more efficient. It is widely used in mobile devices, cryptocurrency, and modern web encryption protocols.
- DSA (Digital Signature Algorithm): A federal standard for digital signatures, DSA is used to authenticate messages and verify the identity of the sender. It generates digital signatures but is not used for encryption. DSA is commonly found in digital certificates and secure email systems.
- Diffie-Hellman Key Exchange: A protocol used for securely exchanging cryptographic keys over a public channel. While Diffie-Hellman itself does not encrypt data, it enables two parties to establish a shared secret key that can be used with symmetric encryption algorithms like AES.
- ElGamal Encryption: Based on the Diffie-Hellman key exchange, ElGamal is an encryption algorithm used for securing messages. It offers a high level of security and is often used in cryptosystems where key exchange and encryption are needed, including some versions of PGP.
- EdDSA (Edwards-curve Digital Signature Algorithm): A variant of DSA that uses elliptic curves for creating digital signatures. It is designed to be faster and more secure than traditional DSA, and is increasingly adopted in modern cryptographic systems, such as in blockchain and secure messaging protocols.
- PAKE (Password-Authenticated Key Exchange): PAKE protocols allow two parties to securely establish a shared key using only a password. This method offers a layer of protection against brute-force attacks, with implementations like SRP (Secure Remote Password) being used in secure password-based authentication systems.
- PGP (Pretty Good Privacy): While PGP combines both symmetric and asymmetric encryption, its key management relies on RSA or ECC for the secure exchange of encryption keys and digital signatures. PGP is widely used for secure email communication and data encryption.
Asymmetric cryptography solves the key exchange problem, allowing secure communication even in open networks. However, its slower performance limits its use for encrypting large data volumes, where symmetric encryption is preferred.
The Symmetric and Asymmetric cryptography combined approach, a symmetric key is used to encrypt and decrypt data, while asymmetric encryption is used to securely exchange the symmetric key. The public key encrypts the symmetric key, and the private key decrypts it.
This hybrid approach is common in secure communication systems, such as SSL/TLS, where asymmetric cryptography is used for the initial exchange of a symmetric key, and symmetric encryption is used for the actual data transfer. The combination offers the performance benefits of symmetric encryption with the security benefits of asymmetric key exchange.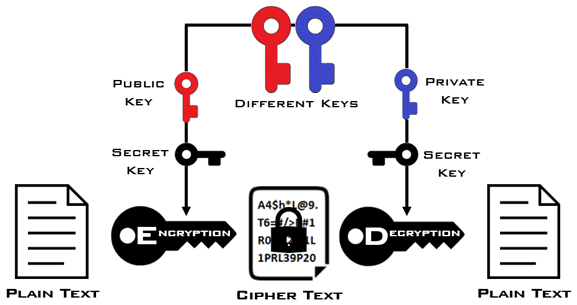
Example Application in Python
| # Filename: symmetric-asymmetric.py from cryptography.hazmat.primitives import hashes, serialization from cryptography.hazmat.primitives.kdf.pbkdf2 import PBKDF2HMAC from cryptography.hazmat.primitives.asymmetric import padding from cryptography.fernet import Fernet import base64 # --- Symmetric Encryption (Fernet) --- # Shared password and salt password = b"secret" # Shared key salt = b"salt1234" # Salt (should be consistent) # Derive a symmetric key using PBKDF2HMAC kdf = PBKDF2HMAC( algorithm=hashes.SHA256(), length=32, salt=salt, iterations=100000, ) symmetric_key = base64.urlsafe_b64encode(kdf.derive(password)) # Symmetric key for Fernet cipher = Fernet(symmetric_key) # Encrypt a message message = b"Hello, World!" encrypted_message = cipher.encrypt(message) print(f"Encrypted message: {encrypted_message}") # --- Asymmetric Encryption of the Symmetric Key --- # Load the public key from file with open("public_key.pem", "rb") as f: public_key = serialization.load_pem_public_key(f.read()) # Encrypt the symmetric key using the public key encrypted_symmetric_key = public_key.encrypt( symmetric_key, padding.OAEP( mgf=padding.MGF1(algorithm=hashes.SHA256()), algorithm=hashes.SHA256(), label=None ) ) print(f"Encrypted symmetric key: {encrypted_symmetric_key}") # --- Decrypt the Symmetric Key using Private Key --- # Load the private key from file with open("private_key.pem", "rb") as f: private_key = serialization.load_pem_private_key(f.read(), password=None) # Decrypt the symmetric key decrypted_symmetric_key = private_key.decrypt( encrypted_symmetric_key, padding.OAEP( mgf=padding.MGF1(algorithm=hashes.SHA256()), algorithm=hashes.SHA256(), label=None ) ) # Check if decrypted symmetric key matches the original symmetric key assert decrypted_symmetric_key == symmetric_key # --- Decrypt the Message --- # Create a Fernet cipher using the decrypted symmetric key cipher_decrypt = Fernet(decrypted_symmetric_key) # Decrypt the message decrypted_message = cipher_decrypt.decrypt(encrypted_message) print(f"Decrypted message: {decrypted_message.decode()}") |
Output:
| $ python symmetric-asymmetric.py Encrypted message: b'gAAAAABm2-XfCF99EO-cKbRent3x78bYpz83RfhNgyzDx4dJL2TMAtqzzI3arBPLJLQ9PAvluF_Q-txKmNss-sbGpB0ZTXwJ9g==' Encrypted symmetric key: b'M\xdc\x14\xe1\xdb{n\xbfy\x0f\xe3*\\`\xc8\xde\xd9\x93\xa8v\xec\x81\xae\x17\\E\xfdG`J\x15\xb6\ x1e\tS\x8d2\x00-\xec\xc3\xe7Z\x8cw\xb6\xca\xed:\xee\x00\xb6\xfbPI\x05s\xf5\x86U\x87\x0bU\xf4\n.N{\xe7.\x04\xaf7\x87p\xb 9\xb0\n\xcb\xfe\xa3l\x82\xe0\xda~5#\xe2D\xe7,\xa6\x91B\xda\x15F\xd5\x1f\xc3~w\x98\xdd\x1a&\x06\xc0\x86\xc4\xd7\x81\x84\ xe6{\x1e\x89,\t\xee-\x17>\x9c\xed\x98Y~\x1bm\x0b\x99\xd0\xd4\xae\r\xb1\x93\xb7Pz\x07j\xf1!U\x97\xfc\x9dA>\x8cs\xd53\xbf \x8f\xde\xfcsj\xe2\xc5P$\x89\x94\x9a\xe6\xe0\xf6:\xd3\xb1\xa8\xbe\x98\xb4\xe4\xfc\xd6\xad\xb79\xe0F\xa08\xaadN\x85\x07\ x11imY\x94\xd1H\x9dC3{\x84\xeePg\xec\xf5a\xa8\x8e)!k\xf8\xff[\xdb\xb7\xd3\xfb\x83\xf0L\x1c-U\x8bhR{hz\x0b2\r \t;\xcb\xb 1f\xca3\xdd\xd8;\xd6xL\xeb\xa3\x8e' Decrypted message: Hello, World! |
Examples of Symmetric and Asymmetric Cryptography Combined
- TLS (Transport Layer Security): TLS is a widely used protocol that secures communication between web servers and clients. It uses asymmetric encryption (usually RSA or ECC) to securely exchange a symmetric key during the initial handshake, and then symmetric encryption (AES) to encrypt the bulk of the data transmitted during the session. This combination provides both security and efficiency.
- SSL (Secure Sockets Layer): The predecessor to TLS, SSL also uses asymmetric encryption (RSA) for key exchange and symmetric encryption (such as 3DES or AES) for securing data transmission. SSL has been deprecated in favor of TLS due to various vulnerabilities, but the combination of encryption techniques remains similar.
- PGP (Pretty Good Privacy): PGP secures emails and files by using asymmetric encryption (RSA or ECC) to encrypt a randomly generated symmetric key (e.g., IDEA, AES). The symmetric key is then used to encrypt the actual message or file. The recipient uses their private key to decrypt the symmetric key and then decrypts the message with the symmetric key.
- S/MIME (Secure/Multipurpose Internet Mail Extensions): S/MIME is an email encryption standard that combines asymmetric encryption (RSA) to protect the key exchange with symmetric encryption (AES or 3DES) for securing the email content. It also supports digital signatures for authenticity and integrity.
- IPSec (Internet Protocol Security): IPSec is a suite of protocols used to secure internet communication at the IP layer. It typically uses asymmetric encryption (like RSA) for exchanging session keys during the initial setup, and symmetric encryption (like AES) for encrypting the actual data payloads in VPNs (Virtual Private Networks).
- Hybrid Encryption in Messaging Apps (e.g., WhatsApp): Modern messaging apps, like WhatsApp, use a combination of asymmetric encryption (typically with protocols like the Signal Protocol that uses ECC) to exchange keys and authenticate users. Once a secure session is established, the actual messages are encrypted with symmetric encryption (AES or ChaCha20), allowing for fast and secure communication.
- SSH (Secure Shell): SSH provides secure access to remote servers by using asymmetric encryption (RSA or DSA) to authenticate users and exchange session keys, followed by symmetric encryption (AES or Blowfish) to encrypt the data transmitted during the session. This approach ensures both security and performance for remote connections.
- Hybrid Cloud Encryption: In many cloud security models, asymmetric encryption (e.g., RSA) is used to securely distribute a symmetric key, which is then used for encrypting large volumes of data stored in or transmitted to the cloud. This model ensures that both the secure distribution of keys and efficient encryption of data are managed.
Combining symmetric and asymmetric cryptography leverages the strengths of both methods, ensuring both security and efficiency in encrypted communication. The symmetric key ensures fast data encryption, while the asymmetric method ensures the secure exchange of this key.
The Symmetric and Asymmetric cryptography with Digital Signature approach, symmetric encryption is used to encrypt and decrypt data. Asymmetric encryption is used to exchange the symmetric key securely. A digital signature is created by hashing the encrypted data to generate a digest, which is then signed using the sender's private key. The recipient verifies the signature using the sender’s public key.
This method enhances the security and integrity of data transmission by ensuring not only confidentiality (through symmetric encryption) but also authenticity and integrity (through digital signatures). It is widely used in secure email communication, financial transactions, and legal documents where both security and verification are critical. Digital signatures confirm the sender's identity and ensure that the data has not been tampered with.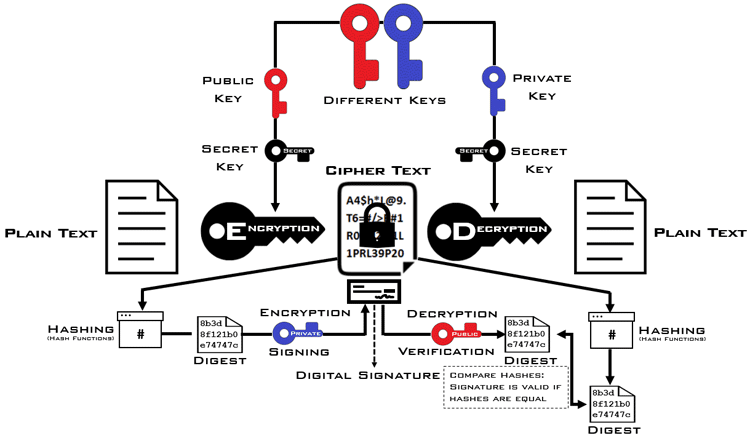
Example Application in Python
| # Filename: symmetric-asymmetric-digital-signature.py from cryptography.hazmat.primitives import hashes, serialization from cryptography.hazmat.primitives.kdf.pbkdf2 import PBKDF2HMAC from cryptography.hazmat.primitives.asymmetric import padding from cryptography.hazmat.primitives.asymmetric import utils as asym_utils from cryptography.hazmat.primitives import hashes from cryptography.fernet import Fernet import base64 # --- Symmetric Encryption (Fernet) --- # Shared password and salt password = b"secret" # Shared key salt = b"salt1234" # Salt (should be consistent) # Derive a symmetric key using PBKDF2HMAC kdf = PBKDF2HMAC( algorithm=hashes.SHA256(), length=32, salt=salt, iterations=100000, ) symmetric_key = base64.urlsafe_b64encode(kdf.derive(password)) # Symmetric key for Fernet cipher = Fernet(symmetric_key) # Encrypt a message message = b"Hello, World!" encrypted_message = cipher.encrypt(message) print(f"Encrypted message: {encrypted_message}") # --- Asymmetric Encryption of the Symmetric Key --- # Load the public key from file with open("public_key.pem", "rb") as f: public_key = serialization.load_pem_public_key(f.read()) # Encrypt the symmetric key using the public key encrypted_symmetric_key = public_key.encrypt( symmetric_key, padding.OAEP( mgf=padding.MGF1(algorithm=hashes.SHA256()), algorithm=hashes.SHA256(), label=None ) ) print(f"Encrypted symmetric key: {encrypted_symmetric_key}") # --- Decrypt the Symmetric Key using Private Key --- # Load the private key from file with open("private_key.pem", "rb") as f: private_key = serialization.load_pem_private_key(f.read(), password=None) # Decrypt the symmetric key decrypted_symmetric_key = private_key.decrypt( encrypted_symmetric_key, padding.OAEP( mgf=padding.MGF1(algorithm=hashes.SHA256()), algorithm=hashes.SHA256(), label=None ) ) # Check if decrypted symmetric key matches the original symmetric key assert decrypted_symmetric_key == symmetric_key # --- Decrypt the Message --- # Create a Fernet cipher using the decrypted symmetric key cipher_decrypt = Fernet(decrypted_symmetric_key) # Decrypt the message decrypted_message = cipher_decrypt.decrypt(encrypted_message) print(f"Decrypted message: {decrypted_message.decode()}") # --- Digest and Sign the Digest with Private Key --- # Create a digest of the encrypted message digest = hashes.Hash(hashes.SHA256()) digest.update(encrypted_message) message_digest = digest.finalize() # Print the hash (digest) of the encrypted message print(f"Hash of encrypted message: {message_digest.hex()}") # Sign the digest using the private key signature = private_key.sign( message_digest, padding.PSS( mgf=padding.MGF1(hashes.SHA256()), salt_length=padding.PSS.MAX_LENGTH ), asym_utils.Prehashed(hashes.SHA256()) # Use pre-hashed digest ) print(f"Signature: {signature}") # --- Verify the Signature using Public Key --- # Verify the signature using the public key try: public_key.verify( signature, message_digest, padding.PSS( mgf=padding.MGF1(hashes.SHA256()), salt_length=padding.PSS.MAX_LENGTH ), asym_utils.Prehashed(hashes.SHA256()) # Pre-hashed digest ) print("Signature verified successfully!") except Exception as e: print(f"Signature verification failed: {e}") # --- Hash from Signature Verification --- # Extract and print the hash value from the signature (recreating the digest from encrypted message) new_digest = hashes.Hash(hashes.SHA256()) new_digest.update(encrypted_message) recreated_message_digest = new_digest.finalize() # Print the recreated hash of the encrypted message print(f"Recreated hash of encrypted message: {recreated_message_digest.hex()}") # --- Compare Digests --- if recreated_message_digest == message_digest: print("The original hash and recreated hash match!") else: print("The original hash and recreated hash do not match!") |
Output:
| $ python symmetric-asymmetric-digital-signature.py Encrypted message: b'gAAAAABm2-fgbjjXM-87fjVDi-O9yL_SvbPoILKqXk3u9aF7-xYPOC8Wga531_CtP10Dpfg5oWlvr71wFIG0WFADpUXVL22iXQ==' Encrypted symmetric key: b'01\x1d?G\x18\xd3\xc5\x8e\xf0]\xb6~\xc6\x1fI\xfc\x813\xea@\xf3\xd6\xf6\x9cF\xab\x9f\xc3*e\xff \x16zhw\xf4\xc90\x81\xe8\xa6\x9a\x03\x00\x11\xd6.4\xc4\x0c\xff<\xc8\x9b\x8f\xc8\x94\xfb\x83\x07+\x8e\xf92\xbf!\xda2\xd7 \xc9\xda\x1a\xfbm7\x04\xbcH\xf8\x01[1\x0b\x1d\xbf\xf4P\x9d\xc9\x90\xb6\x02\xd5\x90u\xe8\xa2\x03\x96{\x808S\r\x93\x10\xa 3\x83q\xc3\xf70n\n\x94\x13A\x8e\xfa\xfc\xc3\xe2\x1b40\xca\x81\rj9\x1e\xe0)Fw\xad\x08\xf5aG\xa0[(\xac\x8f\xbc\x87=.e\xef \xa7y\x89\x99\x9f\xd5\r7\xac\x1c\xe5w\x18l\xb8\x89>\xd7\x1e\xd9\xd1\xaa\x8b\\\xa8\xaa>2-\x87MpDV\x05\xd7)a\xd7\x806\x88 \x97\xce\xfdf\xa8\x01L\x9b\x03\xda\xc5\x05\t\x95\xd1\xec{\x8b\xb7Q\xb1W\xf0\xd3i#\xcc`vt\xef\xc1\x9bS\xee\x06\x13\x8f}\ xa4l=\xd9\xb5o\xc0\n\xa9pQ\xca\x91\xb4\xbd\xd3\xa0\xd6\xf7o\xf3g\xbf' Decrypted message: Hello, World! Hash of encrypted message: 7d085ac3b489fb88839ae1023f9b0da1a984b72c2d72dc99f3a5c956a34b6480 Signature: b"m\xda\xb2j\xc7\x89\xa5\x15\x00\xfb9?\xfb\xdad\xa2\xd8'\xfb\x9fl't\x1a\x87\xdb9v,><\xe5\x12E\xa1\x98\x0b\xb f\x97 \xfc \x108\x0f\x13\x12hyR\xb1\x97\x85\x89\xc6\x9dD\xbf\x97\xd7\x1c\x1d \xf2pEs\x90\x9b.\xad\xb4\x94\xb6s\xef{Yfb\ xff\xc0\x83\xb7\r/\xc8\x01\xc0evk\xce[8\xd9\x85\xa4\x19\xb77|\xeb\x99\xfa\x80\xd7\xc2wBA\x802c\x92&\xf5\x06\xa9K\xed\xb f\x85B\xa5\xc0Z<\xaa\xa4\x1a\xc2\xb4\xce\x18\xfa\x90\x08\xb0\xa5\\\x17\xfb\x960\xaa\xa4\xf4\xfc\xa2u7\xea\x9d<A\xe0\x9b '\xd9!\t\\d%\xa5\xbeGF\xd0\x80h\xa5\xa6\x01)\x94j\x88\xbd[X\xbe\xd6[xt:J\x0fb\xdd\x14\x0c\xd2bcQe;\x0ce\xf5\tM\xd5N\xd0 \x8d\x15\xcf$lz\xe6&X\xd7TU\xe83\x12O\xa2d\x1aW\xa4\x82?\xd7\xfd\xb9\xa4\xb67\xd8\x84=\x10\xf1\x1d\x91\xc1*\x82[\xe9\x0 6\x92u/\xba;K" Signature verified successfully! Recreated hash of encrypted message: 7d085ac3b489fb88839ae1023f9b0da1a984b72c2d72dc99f3a5c956a34b6480 The original hash and recreated hash match! |
Example Signature Verification Application in Python
| # Filename: symmetric-asymmetric-verify-signature.py from cryptography.hazmat.primitives import hashes from cryptography.hazmat.primitives.asymmetric import padding from cryptography.hazmat.primitives import serialization from cryptography.hazmat.primitives.asymmetric import utils as asym_utils # Provide the actual signature value signature = b'\x16F\x1b\x17\xd6\xfc1s\x94p\x14\xd3]y\x85O\xaf\xdbF\x072\x06_\xe9C\xdcr\xf9\x00\xf2\x15\x08\xdd\xe2\x08\ xe0\xa4\xab1\xdd\x0c{\xb2d\x06\xe3\xbb\xcf\xb2V\xcfTf\x12.Qn\x0e\xddL#\xed\x06\t\x9b1\xcd\xfe\xd5\xc7-\xae\x95c\xf3\x07 c\x82\x98G\xd4\x85\xe2\x03P\xf4m:k\x81\x98G\xcd\x8f\xea\xbf\xe56\x9c\x97\x86\xf4\xbf\xdaD\xd0\'X\xa2Y?-\xad\x11\n;\xbcx .\x87\x89\xc0\xc1M\xd3\xc4\xad\xa6\xca\xcd\xf4\x8fA\xeb\x96\x14V\x16\xc8i\x82\xafqR\xe8\xda\x88\xb0\x12\xed\xdd\x98\x15 \xf0\\"*\\X\x8bmj\xb2G.\xfb\x90n\xe2{\xc2 \xcc&\xd5\x8f[\xb7\x82`\xae\n(GxR \x8e\x03u\xed&\x05HW\xaa.\xa8\x08\xf3r\xdc\ xb8p9\xed\xc2\x82\xf7\n\xe0\xd3\x1c\x0f\xbeS\xb3\x06\xc3\xdfRWE=\x92b\xcd\xb6\x9f(\xe5\xcd>\xde\x99\xabh\xf4\xb9\x02\x0 8\xf9\xf9\xc1\xdcx\x99\x03>\xc7\xcbt\'d\x8f\t' # Provide the encrypted message to verify the signature for encrypted_message = b"gAAAAABm3xLMRSt5O6MNHMIZFg2nLK2MXBw8CfSelwPXYSd75Nz2ZriHNH2zK6_XnEPLCUS6Zi8eCbmeGx1F4rujhemmC9lqzg==" # Use the actual encrypted message here # Load the public key from file with open("public_key.pem", "rb") as f: public_key = serialization.load_pem_public_key(f.read()) # Recompute the digest (hash) of the encrypted message digest = hashes.Hash(hashes.SHA256()) digest.update(encrypted_message) recomputed_digest = digest.finalize() # Print the recomputed digest (this is the hash of the encrypted message) print(f"Recomputed digest (hash) of the encrypted message: {recomputed_digest.hex()}") # --- Verify the Signature using Public Key --- # Verifying the signature: It will internally check if the recomputed digest matches the one that was signed try: public_key.verify( signature, recomputed_digest, # The precomputed digest padding.PSS( mgf=padding.MGF1(hashes.SHA256()), salt_length=padding.PSS.MAX_LENGTH ), asym_utils.Prehashed(hashes.SHA256()) # Pre-hashed digest ) print("Signature verified successfully! The digests match.") except Exception as e: print(f"Signature verification failed: {e}") |
Output:
| $ python symmetric-asymmetric-verify-signature.py Recomputed digest (hash) of the encrypted message: f38803814edcaec2b5552cfdc04a046a0f20ce3776c8002c5cc637beac66e806 Signature verified successfully! The digests match. |
Examples of Symmetric and Asymmetric Cryptography with Digital Signature
- PGP (Pretty Good Privacy): PGP uses symmetric encryption (like AES) to encrypt the actual message content, and asymmetric encryption (RSA or ECC) to securely exchange the symmetric key between the sender and receiver. Additionally, PGP uses digital signatures to ensure the authenticity and integrity of the message. The sender creates a hash of the message and signs it with their private key, and the recipient uses the sender's public key to verify the signature.
- S/MIME (Secure/Multipurpose Internet Mail Extensions): S/MIME is an email encryption standard that uses symmetric encryption (AES or 3DES) for the encryption of email content, asymmetric encryption (RSA) for key exchange, and digital signatures to verify the identity of the sender and ensure the message has not been tampered with. The sender signs the email with their private key, and the recipient verifies it using the sender's public key.
- SSL/TLS with Digital Signatures: In secure web communication using TLS, symmetric encryption (AES) is used to protect data in transit, while asymmetric encryption (RSA or ECC) secures the exchange of the symmetric session key. To ensure authenticity, the server signs its certificate (which includes the public key) with a digital signature from a trusted certificate authority (CA). The client can verify the server's authenticity by checking the CA's digital signature.
- Code Signing (e.g., Windows or macOS): Software developers use symmetric encryption to protect files, but for distribution and integrity verification, they sign the code with a digital signature using asymmetric encryption. The developer’s private key signs the code, and users verify the code’s authenticity and integrity using the developer’s public key. This ensures that the code has not been tampered with.
- Bitcoin and Other Cryptocurrencies: In cryptocurrency systems like Bitcoin, asymmetric encryption is used to secure transactions, while digital signatures verify the authenticity of transactions. Users sign transactions with their private key, and others can verify the validity of the transaction using the public key. While the transactions themselves are protected using symmetric encryption for storage, digital signatures ensure the integrity and authenticity of the sender.
- Document Signing (e.g., Adobe PDF Signatures): Many document-signing platforms like Adobe use symmetric encryption to encrypt the content of documents and asymmetric encryption (RSA or ECC) to sign the documents digitally. The sender signs the document with their private key to prove its authenticity, and the recipient can verify it using the sender's public key.
- Secure Electronic Voting Systems: Some e-voting systems use symmetric encryption to secure voter data and asymmetric encryption to exchange keys securely. Digital signatures are used to verify the identity of voters and ensure the integrity of the voting data. The votes are signed with a private key, and the election authority verifies the signature using the voter’s public key.
- Cryptographic Smart Cards: Smart cards, used for secure identification or payment, use symmetric encryption to protect sensitive data. When data is transmitted, asymmetric encryption ensures secure key exchange, while digital signatures confirm the identity of the cardholder. For example, when authenticating with a smart card, the card signs data with its private key, and the system verifies it using the corresponding public key.
The combination of symmetric and asymmetric cryptography, along with digital signatures, ensures a high level of security in terms of confidentiality, integrity, and authenticity. This method is ideal for applications where data must be protected and the sender’s identity and message integrity need to be verified.
By understanding and implementing these cryptographic approaches, individuals and organizations can significantly enhance the security of their communications and data, safeguarding against unauthorized access and cyber threats. Each cryptographic method serves a specific purpose in securing data. Symmetric cryptography offers efficient encryption, asymmetric cryptography solves the key distribution problem, and digital signatures ensure authenticity and integrity. By combining these methods, modern encryption systems can provide both performance and robust security, making them suitable for various secure communication and data protection needs.
How to Generate a Private and Public Key Pair
Generating Private and Public key pair can be used several methods depending on user's preferred tools. Here's how to generate using OpenSSL, Python, and other common tools:
- Using OpenSSL (Command Line): OpenSSL is a widely-used tool for generating keys, certificates, and cryptography in general.
Steps to generate RSA key pair:
- Generate a private key:
$ openssl genpkey -algorithm RSA -out private_key.pem -aes256
This will generate 'private_key.pem' (private key) with AES256 encryption.
For no password, use the following command:
$ openssl genrsa -out private_key.pem 2048 - Extract the public key from the private key:
$ openssl rsa -pubout -in private_key.pem -out public_key.pem
This will generate 'public_key.pem' (public key).
- Generate a private key:
- Using Python (with 'cryptography' library): The 'cryptography' package in Python can be used to generate key pairs easily.
Steps to generate RSA key pair:
- Install the 'cryptography' library:
$ pip install cryptography - Python script to generate RSA key pair:
» Without password:
# Filename: generate-rsa.py
from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.primitives import serialization
# Generate private key
private_key = rsa.generate_private_key(
public_exponent=65537,
key_size=2048,
)
# Serialize and save the private key
with open("private_key.pem", "wb") as f:
f.write(
private_key.private_bytes(
encoding=serialization.Encoding.PEM,
format=serialization.PrivateFormat.PKCS8,
encryption_algorithm=serialization.NoEncryption()
)
)
# Generate public key
public_key = private_key.public_key()
# Serialize and save the public key
with open("public_key.pem", "wb") as f:
f.write(
public_key.public_bytes(
encoding=serialization.Encoding.PEM,
format=serialization.PublicFormat.SubjectPublicKeyInfo
)
)
This will create 'private_key.pem' (private key) without password and 'public_key.pem' (public key).
» With Password:
# Filename: generate-rsa-with-password.py
from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.primitives import serialization
from cryptography.hazmat.primitives.kdf.pbkdf2 import PBKDF2HMAC
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import hashes
# Set password for encrypting the private key
password = b"private_key_password_here" # Password should be in bytes
# Generate private key
private_key = rsa.generate_private_key(
public_exponent=65537,
key_size=2048,
)
# Serialize and save the private key with password encryption (PKCS8 with AES256)
with open("private_key.pem", "wb") as f:
f.write(
private_key.private_bytes(
encoding=serialization.Encoding.PEM,
format=serialization.PrivateFormat.PKCS8,
encryption_algorithm=serialization.BestAvailableEncryption(password)
)
)
# Generate public key
public_key = private_key.public_key()
# Serialize and save the public key (no password needed for public key)
with open("public_key.pem", "wb") as f:
f.write(
public_key.public_bytes(
encoding=serialization.Encoding.PEM,
format=serialization.PublicFormat.SubjectPublicKeyInfo
)
)
This will create 'private_key.pem' (private key) with password and 'public_key.pem' (public key).
- Install the 'cryptography' library:
- Using SSH Keygen (for SSH purposes): If keys for SSH (Secure Shell) is needed, use the 'ssh-keygen' command:
Step to generate RSA key pay:
$ ssh-keygen -t rsa -b 4096 -f ssh_key
This will create 'ssh_key' (private key) and 'ssh_key.pub' (public key).
- Using GPG (GNU Privacy Guard): GPG can be used to generate key pairs for encryption and signing.
Steps to generate key pay:
- Start the 'gpg-agent' using the following command:
$ gpg-agent --daemon - Generate key pair using the following command:
$ gpg --full-generate-key - Follow the prompts to select the type of key (RSA, ECC, etc.), key size, and expiration date.
- List keys (both public and private) using the following commands:
- List public keys:
$ gpg --list-keys
This will show the public keys in keyring.
- List private keys:
$ gpg --list-secret-keys
This will show secret (private) keys.
- List public keys:
- Export the public or private keys, using the following commands:
- Export public key:
$ gpg --export -a " This email address is being protected from spambots. You need JavaScript enabled to view it. " > public_key.asc - Export private key:
$ gpg --export-secret-keys -a " This email address is being protected from spambots. You need JavaScript enabled to view it. " > private_key.asc
This will create ASCII-armored (.asc) versions of the keys, which can be back up or share as needed.
- Export public key:
- Start the 'gpg-agent' using the following command:
Each method has specific use cases, and choose based on user's need for security, cryptography, or communication.
- For encryption tasks, OpenSSL or the Python 'cryptography' library are good choices.
- For SSH connections, 'ssh-keygen' is the standard tool.
- For signing and encrypting email, GPG is commonly used.
Conclusion
Cryptographic approaches are fundamental to modern security protocols and essential for maintaining security and trust in everything from personal data to global and digital communications. Symmetric encryption offers speed and efficiency but struggles with key distribution. Asymmetric encryption solves this problem with secure key exchange but at the cost of performance. Hybrid cryptography blends these techniques, ensuring both security and speed, while digital signatures add another layer of trust, verifying the authenticity and integrity of the information. By combining the strengths of symmetric and asymmetric cryptography along with digital signatures and hash functions, modern cryptographic systems can:
- Ensure Confidentiality: Protect data from unauthorized access using encryption.
- Provide Integrity: Verify that data has not been altered during transmission.
- Authenticate Identities: Confirm the identities of the communicating parties.
- Enable Non-Repudiation: Prevent senders from denying their involvement in a transaction.
The synergy of these methods allows for secure, efficient, and reliable communication even over insecure networks like the internet. These cryptographic techniques provide a robust framework for protecting sensitive information in a world increasingly dependent on digital communication and data security. They are the backbone of secure protocols that protect our privacy, secure online transactions, and enable trust in the digital world. As technology continues to advance and cyber threats evolve, ongoing research and development in cryptography remain critical. Robust cryptographic practices not only protect sensitive information but also underpin the trust and functionality of global digital infrastructures.
Disclaimer: This documentation is intended for educational purposes only. The content provided herein is meant to inform and educate individuals about security practices, techniques, and tools. Security-Science does not support, endorse, or encourage any illegal or unethical activities, including but not limited to unauthorized access to computer systems, networks, or data. Users are advised to apply the knowledge gained responsibly and ensure compliance with all applicable laws and regulations. Security-Science shall not be held liable for any misuse of the information provided.